BZOJ 3730 震波
早上状态完全不在,在有标算的情况下,还是花费了两三个小时才把这道题目做出来。去网上搜了一下,发现好像还没有这道题的题解,出题人自己也没有写详细的题解,所以决定还是写一下题解吧。
这道题目的出题人是Claris(现在好像习惯称呼他为Claris大爷,各种跪烂),他以前也出过一些题目,全都加入到了机房模拟赛之“迈克杯”和“打字比赛”中。我建议他发一些题目到BZOJ上,他说题目太水,都是一眼秒的题目,所以没有上传,直到九月份的某一天,他突然想到了一道题目(就是这题啦),然后花了一个周末的时间弄出了题目、数据和标算,传到了BZOJ上。
中间还发生了一件有趣的事情,当BZOJ上出现这题之后,Claris在纠结自己到底要不要交,Johnson Yip建议他先别交,结果不久后就被Zimpha给AC了,Zimpha表示,这道题目好像和叉姐出的某场模拟赛里面的一道题目差不多。
Claris出完这道题目后,让我猜这道题目的做法,我先是猜树链剖分,他告诉我不是,然后我猜树分治,竟然猜对了,之后Claris就一直怂恿我:“既然你已经知道标算了,就把这道题目给AC了吧……”但是,哪怕知道是树分治,我还是不知道怎么做(主要还是我太弱了),一直拖着。
后来,Claris还专门出了一场"No Wonder Cup"模拟赛,扒了两道题,再加上这题给我们坑,但是我还是没有做出来,直到今天,感觉这题有数据有标算有简略题解,应该能够搞出来,然后就花了一个上午的时间做出了这道题。
闲扯扯了几句,下面上题解:
本体标算是点分治,按照Claris的说法,之所以别人的速度比他的快了一倍,是因为别人都用了树状数组,就他用了线段树,我也用了线段树,然后就垫底了,不过,现在也懒得改了,反正AC了就行。
根据点分治的特点,我们可以知道,一个点最多被log n个重心维护,在点分治的时候,我们需要记录一下维护这个结点的所有重心,以及对于一个特定的重心x,结点y在重心x的哪棵子树里面。
接着对于每一个重心,我们维护k+1棵线段树,k是重心x的子树个数,首先,第1棵线段树维护以重心x为根的子树中,与其距离为d的结点的权值和,剩下的k棵线段树分别维护第k棵子树中,到点x距离为d的结点的权值和。
修改的时候,我们需要依次修改维护该结点的log n个重心对应的线段树,以及该结点在这log n个重心中的子树线段树,查询的时候,我们需要查询维护该结点的log n个重心,如果这些重心距离该结点的距离w[k]小于y,那么就再加上这些重心的权值,并且,查询和重心的距离小于等于y-w[k]的所有结点的权值和,但是,这中间有一点小问题。
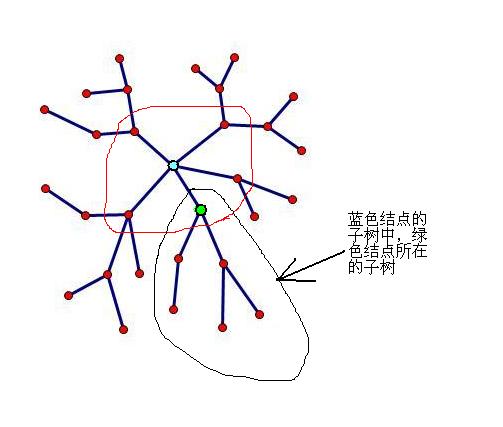
如图,绿色节点是我们要查询的结点,蓝色结点是其所属的一个重心,我们需要查询与绿色节点的距离差值为2的所有点的权值,也就是和蓝色节点距离差为1的所有结点的权值,但是,我们发现,绿色结点的权值被算了两遍,所以,我们需要减去蓝色节点的所有子树中,绿色结点所在的子树中,和蓝色节点距离差值为1的点的权值。
最后的一点小问题就是,因为我太懒,作死用了vector,导致在本机上测试被卡,不过BZOJ上的表现还是可以的(虽然成功垫底),没有被卡掉。
附:
Claris的题解:

My Code:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 | #include <cstdio>#include <algorithm>#include <iostream>#include <cstring>#include <cstdlib>#include <utility>#include <bitset>#include <vector>#include <string>#include <stack>#include <queue>#include <ctime>#include <cmath>#include <list>#include <map>#include <set>#define pb push_backusing namespace std;typedef long long ll;typedef double D;typedef pair<int,int> pr;const int N=200010;const int M=5000100;vector<int > v[N],u[N],w[N];int n,m,val[N];int g[N],to[N],nxt[N],tot=1;int f[N],size[N],sz,cur,num;int son[M][2],len;int head[N],root[N];ll sum[M],lastans;bool ok[N];void Max(int &x,int y) {if (x<y) x=y;}void read(int &a) { char ch; while (!((ch=getchar())>='0'&&ch<='9')); a=ch-'0'; while ((ch=getchar())>='0'&&ch<='9') (a*=10)+=ch-'0';}void addedge(int x,int y) { to[++tot]=y; nxt[tot]=g[x]; g[x]=tot; ok[tot]=1; to[++tot]=x; nxt[tot]=g[y]; g[y]=tot; ok[tot]=1;}void ins(int &i,int l,int r,int x,int y) { if (!i) i=++len; sum[i]+=y; if (l==r) return; int mid=(l+r)>>1; if (x<=mid) ins(son[i][0],l,mid,x,y); else ins(son[i][1],mid+1,r,x,y);}ll ask(int i,int l,int r,int x,int y) { if (!i||x>y) return 0; if (x<=l&&y>=r) return sum[i]; int mid=(l+r)>>1;ll ans=0; if (x<=mid) ans+=ask(son[i][0],l,mid,x,y); if (y>mid) ans+=ask(son[i][1],mid+1,r,x,y); return ans;}void find(int x,int fat) { int k; size[x]=1; f[x]=0; for (k=g[x];k;k=nxt[k]) { if (to[k]==fat) continue; if (!ok[k]) continue; find(to[k],x); size[x]+=size[to[k]]; Max(f[x],size[to[k]]); } Max(f[x],sz-size[x]); if (f[x]<f[cur]) cur=x;}void dfs(int x,int fat,int dep) { v[x].pb(cur); u[x].pb(num); w[x].pb(dep); ins(head[cur],1,n,dep,val[x]); ins(root[num],1,n,dep,val[x]); for (int k=g[x];k;k=nxt[k]) if (to[k]!=fat&&ok[k]) dfs(to[k],x,dep+1);}void solve(int x) { int i,j,k; for (k=g[x];k;k=nxt[k]) if (ok[k]) num++,dfs(to[k],x,1); for (k=g[x];k;k=nxt[k]) if (ok[k]) { ok[k^1]=0; f[0]=sz=size[to[k]]; find(to[k],cur=0); solve(cur); }}ll query(int x,int k) { ll ans=ask(head[x],1,n,1,k)+val[x]; int i,sz=v[x].size(); for (i=0;i<sz;i++) { if (w[x][i]<=k) ans+=val[v[x][i]]; ans+=ask(head[v[x][i]],1,n,1,k-w[x][i])-ask(root[u[x][i]],1,n,1,k-w[x][i]); } return ans;}void modify(int x,int y) { int i,sz=v[x].size(),t=y-val[x]; val[x]=y; for (i=0;i<sz;i++) { ins(head[v[x][i]],1,n,w[x][i],t); ins(root[u[x][i]],1,n,w[x][i],t); }}int main() { int i,k,x,y; read(n); read(m); for (i=1;i<=n;i++) read(val[i]); for (i=1;i<n;i++) { read(x); read(y); addedge(x,y); } f[0]=sz=n; find(1,cur=0); solve(cur); for (i=1;i<=m;i++) { read(k); read(x); read(y); x^=lastans; y^=lastans; if (k==0) printf("%lld\n",lastans=query(x,y)); else if (k==1) modify(x,y); } return 0;} |
2015年1月15日 21:50
倒一被我抢了。。我加了2进制读入才过的。。。
2015年1月16日 12:19
@Newnode: 2333
2022年8月25日 20:25
Meghalaya Board Model Paper 2023 Class 12 Pdf Download with Answers for Bengali Medium, English Medium, Hindi Medium, Urdu Medium & Students for Small Answers, Long Answer, Very Long Answer Questions, and Essay MBOSE Question Paper Class 12 Type Questions to Term1 & Term2 Exams at official website. New Exam Scheme or Question Pattern for Sammittive Assignment Exams (SA1 & SA2): Very Long Answer (VLA), Long Answer (LA), Small Answer (SA), Very Small Answer (VSA), Single Answer, Multiple Choice and etc.