BZOJ 3683 Falsita
最近状态极差，效率极低……先是CF上的一道lct裸体坑了我足足两天，然后又被现在这道题给坑了五六个小时，各种不爽……
题目大意：
一棵以1号结点为根的n个结点的树，每个点都有一个点权v[i]，两个点x和y可以在它们的lca处，耗费w[x]+w[y]的代价达成共识，现在要求三种操作：1.每个点权值增加delta 2.以某点为根的子树中所有节点的权值都增加delta 3.查询在一个结点达成共识时所需要的代价的期望值
首先，我们规定几个概念：
sz[x]表示以结点x为根的子树中结点个数
SZ[x]表示lca为x结点的方案数
sum[x]表示以结点x为根的子树中结点的权值和
v[x]表示结点x的权值
P(x)表示x结点所有子节点的集合
那么对于一个结点x，其答案为 } sum[i]*(sz[x]-sz[i])}\ %2B\ v[x]*(sz[x]-1))
除以SZ[x]。
要注意的是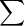
并不包括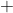
后面的这一部分，也就是说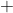后面的部分是独立计算的。
前面这个很长的式子计算出了所有的可能的情况，我们来证明这一点，首先，如果两个结点的lca是x，那么这两个结点就不能够在x的同一棵子树当中，如果选择了子树i中的一个结点，那么只能从剩下的sz[x]-sz[i]个结点中选取另外一个结点，所以，子树i的所有结点都可以被选择sz[x]-sz[i]次。根节点x则需要单独算，一共有sz[x]-1次被选中的可能。
接着，我们需要求出SZ[x]，这个可以在dfs的时候计算出来，我们首先遍历结点x的一个子节点i，那么，SZ[x]+=sz[i]*sz[x]（请注意，这里的sz[x]表示在遍历子树i之前已经遍历的子树的结点总数），因为对于子树i中的每一个结点，都可以任意地从之前遍历过的子树中找到一个结点对应。计算为SZ[x]之后，sz[x]+=sz[i]。
这样是不是就万事大吉了呢？如果只有查询操作的话，确实已经算是完成了，但这道题还有修改操作。我们需要用一些数据结构来维护这棵树，首选自然是链剖+线段树，但是，这一道题目只有区间求和和区间赋值操作，所以用树状数组也足以维护了，而且，相比较线段树，树状数组速度更快，代码量更小。
我们定义：
w[x]为结点x树链剖分后的重儿子
top[x]表示x所属的重链的尾端结点
st[x]表示以结点x为根的子树的dfs序的起始值
ed[x]表示以结点x为根的子树的dfs序的终止值
T(x)表示x结点所有非重儿子结点的集合
接着，我们维护两个树状数组，不妨设为BIT1和BIT2，对于一个结点x，BIT1维护的是sum[w[x]]，而BIT2维护的则是SZ[x]的倍数——如果，以x为根的子树中的所有节点的权值都加上t[x]，那么结点x的答案就需要加上2*t[x]。
另外，我们还需要记录v[x]*(sz[x]-1)，以及}sum[i]*(sz[x]-sz[i]))
，这两个东西可以用同一个数组b来维护。
说了这么多，最后我们需要查询的是
，t[x]的含义如上所述，由BIT2维护，之所以说维护的是SZ[x]的倍数，是因为将式子通分之后，将会变成
。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 | #include <cstdio>#include <algorithm>#include <iostream>#include <cstring>#include <cstdlib>#include <utility>#include <bitset>#include <vector>#include <string>#include <stack>#include <queue>#include <ctime>#include <cmath>#include <list>#include <map>#include <set>using namespace std;typedef long long ll;typedef double D;typedef pair<int,int> pr;const int infi=2147483647;const int mod=1000000007;const D eps=1e-6;const int N=600010;char s[10];int n,m,fa[N],v[N],w[N];int g[N],to[N],nxt[N],tot;int sz[N],st[N],ed[N],top[N],df;ll h[N][2],b[N],SZ[N];int f;void read(int &a) { char ch; while (!(((ch=getchar())>='0'&&ch<='9')||(ch=='-'))); if (ch=='-') a=0,f=-1; else a=ch-'0',f=1; while ((ch=getchar())>='0'&&ch<='9') (a*=10)+=ch-'0'; a*=f;}void addedge(int x,int y) { to[++tot]=y; nxt[tot]=g[x]; g[x]=tot;}void add(int pos,ll x,int k) {while (pos<=n) h[pos][k]+=x,pos+=pos&-pos;}ll sum(int pos,int k) {ll t=0; while (pos>0) t+=h[pos][k],pos-=pos&-pos;return t;}void dfs(int x) { int k; sz[x]=1; for (k=g[x];k;k=nxt[k]) { dfs(to[k]); if (sz[to[k]]>sz[w[x]]) w[x]=to[k]; SZ[x]+=(ll)sz[to[k]]*sz[x]; sz[x]+=sz[to[k]]; }}void dfs2(int x,int y) { st[x]=++df; top[x]=y; if (w[x]) dfs2(w[x],y); for (int k=g[x];k;k=nxt[k]) if (to[k]!=w[x]) dfs2(to[k],to[k]); ed[x]=df;}void modify(int x,ll y) { while (x) { add(st[top[x]],y,0); add(st[x],-y,0); x=top[x]; if (x) b[fa[x]]+=(ll)y*(sz[fa[x]]-sz[x]),x=fa[x]; }}ll query(int x) { ll ans=b[x]; ans+=(ll)(sz[x]-sz[w[x]])*sum(st[x],0); ans+=SZ[x]*sum(st[x],1); return ans;}int main() { int i,x,y; read(n); read(m); for (i=2;i<=n;i++) { read(fa[i]); addedge(fa[i],i); } dfs(1); dfs2(1,1); for (i=1;i<=n;i++) { read(x); modify(i,x); b[i]+=(ll)(sz[i]-1)*x; } for (i=1;i<=m;i++) { scanf("%s",&s); read(x); if (s[0]=='Q') printf("%.6lf\n",(D)query(x)/SZ[x]); else { read(y); if (s[0]=='S') { modify(x,y); b[x]+=(ll)y*(sz[x]-1); } else if (s[0]=='M') { modify(x,(ll)y*sz[x]); add(st[x],y<<1ll,1);add(ed[x]+1,-(y<<1ll),1); } } } return 0;} |
2022年9月03日 18:04
Haryana Board Model Paper 2023 Class 4 Pdf Download with Answers for English Medium, Hindi Medium, Urdu Medium & Students for Small Answers, Long Answer, Very Long Answer Questions, and Essay Type Questions to Term1 & Term2 Exams at official website. Haryana Board Question Paper Class 4 New Exam Scheme or Question Pattern for Sammittive Assignment Exams (SA1 & SA2): Very Long Answer (VLA), Long Answer (LA), Small Answer (SA), Very Small Answer (VSA), Single Answer, Multiple Choice and etc.