BZOJ 3731 Gty的超级妹子树
明天就要月考了,总感觉现在这个时候还在做题不太好……呃,不过既然都已经开始做这题了,如果不AC了它的话,估计我也没有心情去月考了(好吧,我承认这一段是在胡扯233)
下面是正题:
这道题目的做法是块状树套上平衡树,我打的是Treap,感觉还是Treap好打一些,而且为了速度,我作死地打了指针+结构体,调试的时候真的是欲仙欲死。
首先,我们需要将整棵树分成好几个部分,至于怎么分块我就不说了,毕竟网上都应该能够搜到。分块之后,我们就将整棵树(我们定义其为1号树)变成了一棵很小的树,每一个结点都是一个块,我们定义这棵树为2号树。
0.查询
查询的是一棵子树,首先,我们找到查询的结点u,接着,对u所属的那个块中的属于u子树的结点都查询一遍,判断其权值是不是严格大于x。其次,在2号树对1号树中u的子节点所属的块进行查询,因为每一个块都套上了Treap,查询的话还是挺方便的。具体的可以参照下图:
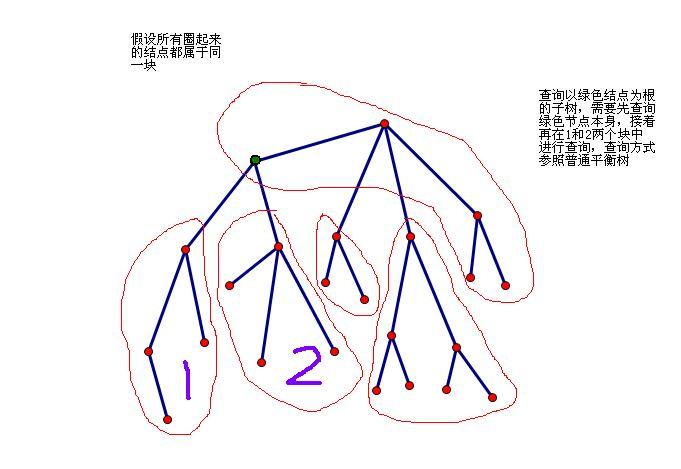
1.修改
把点u的权值改成x,其实等于是在u所属块套上的Treap中,将u这个结点删去,改掉权值之后再将u插入回去,这里有一个坑点,我的Treap是根据每一块的根来算的,也就是说,有a1,a2..ak个结点都位于Treap[a1]中,那么将a1从Treap[a1]中删去之后再插入进去,最后得到的是一棵只有一个结点的Treap。
2.插入
插入一个新结点要分类讨论,如果这个结点的父亲节点所属的块的大小还没有饱和,那么新插入的结点也属于这个块,否则,新插入的结点就是一个新的块,不要忘记将新的块所构成的新结点插入到2号树中。
3.删除
删除操作也是一个麻烦事,我们假设u属于块pos[u]。如果pos[u]==u那么就在2号树中将这个结点和它的父亲结点断开就行了,否则,我们需要将u的所有子节点中属于pos[u]的点都从Treap[pos[u]]中删去然后再插入到新的Treap[pos[u]=u]中。其次,在2号树中,对于那些u子树所构成的块结点,需要将其和pos[u]断开连接,再重新和pos[u]=u连接。
大致就是这个样子,本来这个程序昨天中午就打好了的,调了大概一两个小时,直到后来,极限数据出错概率也只有5%~10%了,那才是最痛苦的时候,小数据大概对拍了半个多小时才拍出了一组数据将我的程序卡掉,结果扔到BZOJ上还是超时了,也不知道在哪里出了问题,直到不久前才发现,原来是对于块的size定义出了问题,为了调试方便,我把每块的大小都定义为了4 TAT。改成了400后就AC了,时间是五秒多,后来一直扩大这个数值,直到每块的size都在6000左右的时候,速度被我提到了1.75秒,感觉再进步就比较麻烦了。
另外,感觉这道题目的这种做法还是有点问题的,我发现如果是菊花图的话,似乎可以卡掉分块做法……不过我也懒得管这么多了,还是乖乖滚去复习月考吧……
Updata:BZOJ 3720 Gty的妹子树 和这道题目同一个出题人,操作比这题少了一个(断裂操作),其他都一样,所以你们都懂得。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 | #include <cstdio>#include <algorithm>#include <iostream>#include <cstring>#include <cstdlib>#include <utility>#include <bitset>#include <vector>#include <string>#include <stack>#include <queue>#include <ctime>#include <cmath>#include <list>#include <map>#include <set>using namespace std;typedef long long ll;typedef double D;typedef pair<int,int> pr;const int infi=2147483647;const int mod=1000000007;const D eps=1e-6;const int N=500010;const int M=100010;const int Q=200010;const int size=6000;struct Treap* null;struct Treap{ Treap *fa,*son[2]; int key,data,sz; void newnode(int x) { data=x; key=rand(); sz=1; fa=son[0]=son[1]=null; } void updata() { sz=son[0]->sz+son[1]->sz+1;} void rotate() { Treap *x=this,*y=x->fa,*z=y->fa; int w=(y->son[0]==x); if (z!=null) z->son[z->son[1]==y]=x; x->fa=y->fa; y->fa=x; if (x->son[w]!=null) x->son[w]->fa=y; y->son[w^1]=x->son[w]; x->son[w]=y; y->updata(); x->updata(); } void insert(Treap *&y) { Treap *x=this; x->sz++; if (y->data>x->data) { if (x->son[1]!=null) x->son[1]->insert(y); else x->son[1]=y,y->fa=x; if (x->son[1]->key<x->key) x->son[1]->rotate(); } else { if (x->son[0]!=null) x->son[0]->insert(y); else x->son[0]=y,y->fa=x; if (x->son[0]->key<x->key) x->son[0]->rotate(); } x->updata(); } Treap* merge(Treap *fat,Treap *x,Treap *y) { if (x==null&&y==null) return null; if (x==null) { y->fa=fat; return y; } if (y==null) { x->fa=fat; return x; } if (x->key<y->key) { x->son[1]=merge(x,x->son[1],y); x->fa=fat; x->updata(); return x; } else { y->son[0]=merge(y,x,y->son[0]); y->fa=fat; y->updata(); return y; } } void clear() { if (this==null) return; else this->updata(); if (this->fa!=null) this->fa->clear(); } void del() { Treap *x=this,*y=merge(x->fa,x->son[0],x->son[1]); x->fa->son[x->fa->son[1]==x]=y; x->fa->clear(); x->sz=1; x->fa=x->son[0]=x->son[1]=null; } int ask(int y) { if (this==null) return 0; Treap *x=this; int ans=0; if (x->data>y) ans++; if (y>=x->data) ans+=x->son[1]->ask(y); else { ans+=x->son[1]->sz; ans+=x->son[0]->ask(y); } return ans; } Treap* findroot() { if (this->fa==null) return this; else return this->fa->findroot(); }};Treap pool[Q];Treap* v[Q];Treap* total;int n,m,w[Q],lastans;int pos[Q],sz[Q],fa[Q];int g[Q],to[N],nxt[N],tot;int G[Q],TO[N],NXT[N],TOT;void read(int &a) { char ch; while (!((ch=getchar())>='0'&&ch<='9')); a=ch-'0'; while ((ch=getchar())>='0'&&ch<='9') (a*=10)+=ch-'0';}void addedge(int x,int y) { to[++tot]=y; nxt[tot]=g[x]; g[x]=tot; to[++tot]=x; nxt[tot]=g[y]; g[y]=tot;}void ADDEDGE(int x,int y) { TO[++TOT]=y; NXT[TOT]=G[x]; G[x]=TOT;}void init() { total=pool; null=total++; null->fa=null->son[0]=null->son[1]=null; null->key=null->data=null->sz=0;}void dfs(int x,int fat) { int cur=pos[x],k; fa[x]=fat; for (k=g[x];k;k=nxt[k]) if (to[k]!=fat) { if (sz[cur]+1<=size) { sz[pos[to[k]]=cur]++; Treap *t=v[cur]->findroot(); t->insert(v[to[k]]); } else ADDEDGE(cur,pos[to[k]]); dfs(to[k],x); }}int query(int x,int y) { int k,ans=0; Treap *t; if (pos[x]==x) { t=v[x]->findroot(); ans+=t->ask(y); for (k=G[x];k;k=NXT[k]) ans+=query(TO[k],y); } else { if (w[x]>y) ans++; for (k=g[x];k;k=nxt[k]) if (to[k]!=fa[x]&&fa[to[k]]==x) ans+=query(to[k],y); } return ans;}void change(int x,int y) { Treap *t; w[x]=y; t=v[x]->findroot(); if (t==v[x]) { if (t->son[0]!=null) t=t->son[0]; else if (t->son[1]!=null) t=t->son[1]; else { v[x]->data=y; return; } } v[x]->del(); t=t->findroot(); v[x]->data=y; t->insert(v[x]);}void add(int fat,int x,int y) { v[x]=total++; fa[x]=fat; addedge(fat,x); w[x]=y; v[x]->newnode(y); if (sz[fat]+1<=size) { sz[pos[x]=pos[fat]]++; Treap *t=v[pos[fat]]->findroot(); t->insert(v[x]); } else { sz[pos[x]=x]++; ADDEDGE(pos[fat],pos[x]); }}void delink(int X,int Y) { int K; if (TO[G[X]]==Y) G[X]=NXT[G[X]]; else for (K=G[X];K;K=NXT[K]) { if (TO[NXT[K]]==Y) { NXT[K]=NXT[NXT[K]]; return; } }}void cut(int x,int loc) { int k; if (pos[x]==x) delink(pos[fa[x]],x); else { v[x]->del(); sz[pos[x]]--; for (k=g[x];k;k=nxt[k]) { if (pos[to[k]]==pos[x]&&to[k]!=fa[x]&&fa[to[k]]==x) cut(to[k],loc); else if (to[k]!=fa[x]&&fa[to[k]]==x&&pos[to[k]]==to[k]) { delink(pos[loc],pos[to[k]]); ADDEDGE(loc,pos[to[k]]); } } sz[pos[x]=loc]++; if (pos[x]!=x) { Treap *t=v[loc]->findroot(); t->insert(v[x]); } }}int main() { int i,x,y,k; init(); for (read(n),i=1;i<n;i++) { read(x); read(y); addedge(x,y); } for (i=1;i<=n;i++) { read(w[i]); v[i]=total++; v[i]->newnode(w[i]); pos[i]=i; } dfs(1,0); for (read(m),i=1;i<=m;i++) { read(k); read(x); x^=lastans; if (k!=3) read(y),y^=lastans; if (k==0) printf("%d\n",lastans=query(x,y)); else if (k==1) change(x,y); else if (k==2) add(x,++n,y); else if (k==3) if (fa[x]) cut(x,x),fa[x]=0; } return 0;} |
2022年8月31日 15:54
Comilla board is another education board working under Secondary and Higher Secondary Education, Bangladesh, and the education board is also successfully completed the Grade 8 terminal examinations at all selected examination test centers at Comilla division, and the Junior School Certificate and Junior Dakhil Certificate terminal examination is a second largest examination in the country. Grade 8 Result Comilla The Comilla Board is also completed those subject wise exams between 1st to 3rd week of November as per schedule announced by School Education department, and there are a huge number of students are participated like as all other educational boards from all districts of the division, right now they are waiting to check JSC & JDC Result 2022 Comilla Board with subject wise marks and total marksheet with final CGPA grade of the student.